A legegyszerűbb körös mintavétel fix sugarú körökkel dolgozik, és ez a módszer tekinthető a területen levő faállomány torzítatlan becslésének.
A fentiekből kiindulva csináltam egy olyan eljárást is, amit "gyűrűfelezés" néven használok, és arról szól, hogy ha ismerjük a mintakörön kívüli első külső fa helyzetét is, akkor a mintakör területe számítható az első külső fa és az utolsó belső mintafa közé rajzolt körrel, mely kör felezi a két fa közti gyűrű területét. Ekkor minden egyes fához olyan gyűrű tartozik, aminek az adott fa a "közepén" áll (idézőjel).
Ez tulajdonképpen a mintakör egydimenziós ábrázolásának a logikus folytatása: ha gyűrűk adódnak hozzá a mintakörhöz az egyes fák belépésével, akkor az utolsó fához tartozó gyűrű területét is úgy kell levezetni, mint az összes többiét korábban.
(Biztos van neve a szakirodalomban, mert kötve hiszem, hogy én találtam volna fel a spanyolviaszkot.)
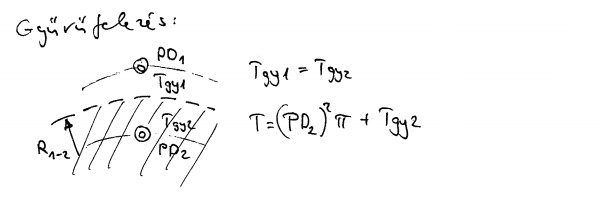
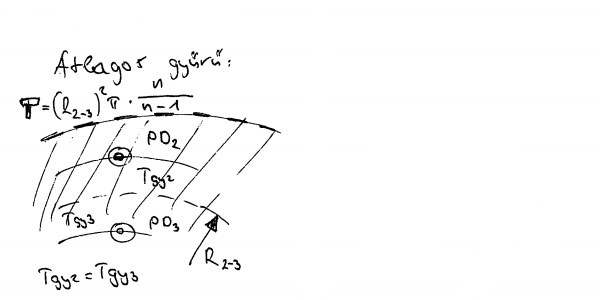
Aztán csináltam egy negyedik eljárást, amiben, ha nem ismerjük a körön kívüli első fát, a körön belüli két legtávolabbi fa közti gyűrűt felező sugarat szoroztam fel n*(n-1)-gyel, azaz az egy fára eső átlagos gyűrű területét használtam. Az "átlagos gyűrű" nevet nyerte.