walden

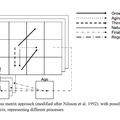
Az osztályozást tehát jó lett volna megoldani automatizálva. Ehhez nem találtam megfelelő klaszterezési eljárást az általam ismert szoftverekben és a rendelkezésre álló pár nap alatt. Olyan osztályozási eljárást, ami:

• eleve létező csoportokat (elemi erdészeti tájrészleteket) tud osztályozni, azaz eloszlásokat osztályoz;
• elválasztja őket az átlagaik alapján;
• kis számú csoportot képez (2-3-4 darabot).

Biztos van ilyen, nem hiszem, hogy a statisztika tudományában fel lehetne találni a spanyolviaszkot, de én pár nap keresgélés után sem találtam ilyet.

Ezért írtam egyet.

A varincia-analízisben a csoportokon belüli és a csoportok közti variancia viszonyát hasonlítják össze. Ezzel mérhető az átlagok eltérése. E csoportosító eljárásban pedig az a cél, hogy olyan csoportokat képezzek, ami minimalizálja a csoportokon belüli variancát és maximalizálja a csoportok közöttit.

A legjobb az lenne (brute force megoldás), ha minden lehetséges 2-3-4 db csoportot eredményező csoportosítási kombinációt meg lehetne vizsgálni, csoporton belüli varianciákat számolni és a legjobbat kiválasztani. De sajnos 92 db erdészeti tájrészletből bődületes számú kombinációban lehet 2-3-4 csoportot képezni, ezért ez nem megoldható.

Olyan megoldást választottam, hogy az algoritmusnak megadtam jellegzetes tájrészleteket, amik egyrészt nagy területűek (a fatermőképesség fafajsori területtel súlyozott varianciája szoros összefüggésben van a területtel, általában a nagy területű tájak dominálnak egy-egy csoportot), másrészt a képzendő csoportokat reprezentálják. Azaz nagy és átlagukban markánsan különböző tájrészleteket választottam ki, 2 vagy 3 darabot. Az algoritmus ezekhez a magokhoz illeszti a többi tájrészletet.

A variancia implicite tartalmazza az ftk-átlagok viszonyait. Annál illesztésnél növekszik a legkevésbé a variancia, ahol az új belépő tájrészlet átlaga a legközelebb van a már létező csoport átlagához, illetve ami kicsi elemszámú.

Tegyük fel, hogy 2db mag van, azaz két csoport képződik.

Az algoritmus az első lépésben hozzápróbálja a magokhoz az összes még be nem sorolt tájrészletet. Minden maghoz kiválasztható az, ami a legkevésbé emeli meg a varianciát a mag-egtáj belső varianciájához képest. Aztán ki kell választani azt a magot, ahol a legkevésbé emelkedett a variancia. Így egy tájrészletet besoroltunk.

A következő lépcsőben van egy 2 elemű csoport és egy 1 elemű. Ezekhez újra hozzápróbálja az összes szabad tájat, mindkét magnál kiválasztja azt, ami a legkevésbé emeli a csoport varianciáját; majd azt a magot, aminél kevésbé emelkedett a variancia.

És ezt így tovább mindaddig, amíg el nem fogy az összes besorolandó tájrészlet.

Kicsit hasonlít a k-means clusteringre, de nem ugyanaz.

Ez az eljárás először a mag körüli kis tájakat gyűjti oda majd, aztán a rizikósabb nagyobb tájak sorsa eldől magától.

Praktikusan akkor jó az osztályozás, ha a képzett csoportok:

• elég nagyok (terület), hogy kerüljön majd beléjük kellő mennyiségű FNM-mintapont, amivel stabil regressziós modelleket lehet szerkeszteni;
• az átlagaiknak elég távolnak kell lenniük, hogy a csoportok elváljanak egymástól (szerintem legalább ftk=2 m3/ha/év különbség, az már 1-2 fatermési osztályt jelent a hagyományos, egyenletes osztásközű fatermési tábláknál).

Az osztályozás jóságát a csoportokon belüli és a csoportok közötti variancia viszonyával lehet mérni. Minél nagyobb a csoportok közti variancia, annál szeparáltabbak a csoportok. Minél kisebb ez a szám, annál inkább összemosódnak a csoportok. A csoportok közti variancia általában a sokaság teljes varianciájának 25-30%-át adta: kb. ennyit javít az osztályozás a későbbi eredmények pontosságán [ez nem pont jó kifejezés].

Czirok István kolléga szakmai tapasztalatai és az előzetes hisztogramok alapján készített egy két csoportos (jobb-gyengébb) osztályozást az Akác mag táblára. Ezt kíváncsiságból összevetettem az algoritmikus eredménnyel. 92 tájrészletből 81 esetében azonos besorolásra jutottunk. A 11 darab eltérés a teljes vizsgálati anyag (a 2005-2014 közt átvezetett erdőtervek) fafajsori területének 4,6%-a. Sikerélmény. További önbizalomra ad okot.

Térképeken ábrázoltuk (Magyar Zsolt tette) a kialakult csoportosítást, és meglepően egybefüggő tömböket adott, és ami ki is válik a tömbökből, az indokolhatóan válik ki (pl. az árterek). Azt hittem, sokkal mozaikosabb lesz.

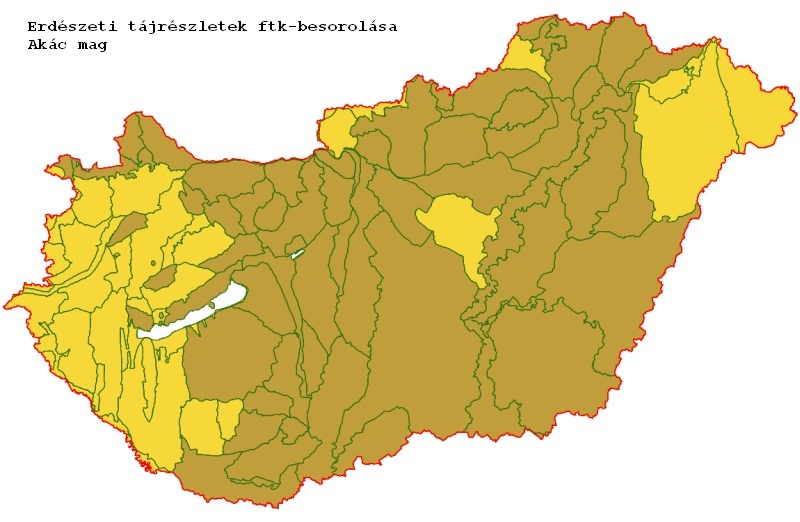
Szerintem többször az van, hogy amikor egy általában jó termőhelyekben gazdag tájon egy fafaj/fafajcsoport gyengébb eredményeket ad, ott általában a konkrétan jó részletekben az értékesebb fafajok vannak, és csak a gyengébb részletekben a betelepített faj (akác esetében volt ez a benyomásom).