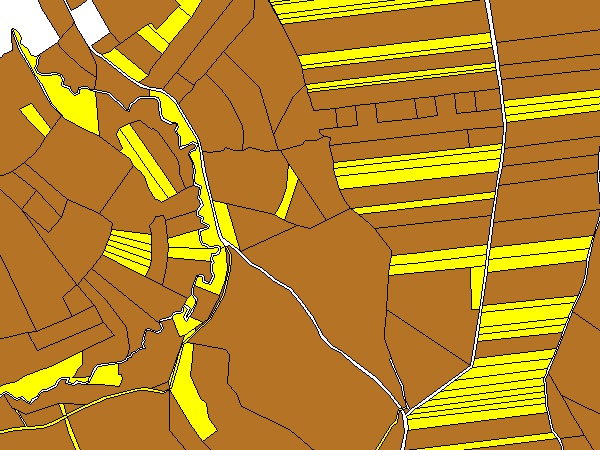
Az Erdőtörvény készülő módosítása (a 2017-es, éppen módosítókkal bombázzák szét a parlamentben, ettől most tekintsünk el), szóval több helyen külön figyelmet szentel a kis méretű, keskeny, nehezen kezelhető részleteknek - azt szeretné, hogy ne legyenek ilyenek, vagy minél kevesebb. Nem szabad ilyet létrehozni vagy kivezetendők a nyilvántartásból. A módosítás pl. a 86. § (1) és 87. § (27) bekezdésekben hivatkozik az erdőrészletek geometriájára: "szélessége átlagosan legalább harminc méter".
Maradjunk a műszaki problémánál.
Az érintett részletek azonosításában a kritikus pont az átlagos szélesség mérése. A részletek digitalizált térképészeti poligonjainak adataiban benne van ez az információ, de nagyon nehéz kinyerni. Ez az "átlagosan x méter" (más helyeken szerepel 20 méteres mérethatár is a definíciókban) - ez nagyon nyűgös fogalom. Ha a részlet geometriája olyan, hogy megrajzolható a hossztengelye, akkor arra állíthatók merőlegesek és ezek mentén az egyes szelvényekben mérhető a részlet szélessége, de a hossztengely nem minden esetben rajzolható meg egyértelműen és intuitív módon. Mi van mondjuk, ha szabályos négyzet alakú a részlet, egyenlő oldalakkal, de az egyik sarkában van egy kis kitüremkedés? Á, hagyjuk.
Talán lehet valamilyen függvényt levezetni a terület és alakszám, vagy a terület és kerület viszonyára, ami a poligon átlagos szélességére adna közelítő információt - gondolta a mérnök. Egy mérnöknek lehetnek nem bizonyított, de kipróbálható módszerei.
Tekintsünk egy téglalap alakú részletet, ennek a szélessége konstans a hossztengelye mentén. Legyenek oldalai a-val és b-vel jelöltek. Ekkor:
- a <= 30
- a*b = TER
- 2*(a+b) = KER
Az egyenletek rövid rendezése után: - KER >= 60 + 20000/30*TER
összefüggés adódik, ami olyan részleteket szűr, ahol a poligon, amit a vele megegyező területű és kerületű téglalappal helyettesítettünk, na ennek az "átlagos szélessége" kisebb, mint 30 méter.
Itt lehet a csúsztatás, hogy helyettesíthető-e a nagyon bizonytalanul definiált "átlagos szélesség" szempontjából egy tetszőleges geometriájú részlet egy téglalappal. De miért ne? A megoldás egészen jól működik, hozza a keskeny részleteket. The power of középiskolás elsőfokú egyenletrendszer. Pontosabban ha értelmezhető úgy az „átlagosan harminc méter széles”, ahogy a módszernek jó, akkor hozza.
Nadrágszíj-parcellák az Őrségben: