Körös mintavételnél a mintába kerülés valószínűsége csak a középponttól mért távolságtól függ, azaz ebből a szempontból a mintakör leegyszerűsíthető egy olyan ábrára, ami egyetlen egyenesen (félszakaszon), a középponttól kifelé indulva csak a fák távolságát mutatja. Nagy átlagban a fák egymás után egyre sűrűbben lépnek be, mert minden egyes fával egy gyűrű adódik hozzá a mintakörhöz, és ha a fák síkban vett, kétdimenziós XY-eloszlása (vagy három dimenziós, ha a terep nem sík, és bonyolítani akarom); tehát ha a fák kb. egyforma területet foglalnak el a mintakörben, akkor ezek a gyűrűk kb. egyforma területűek.
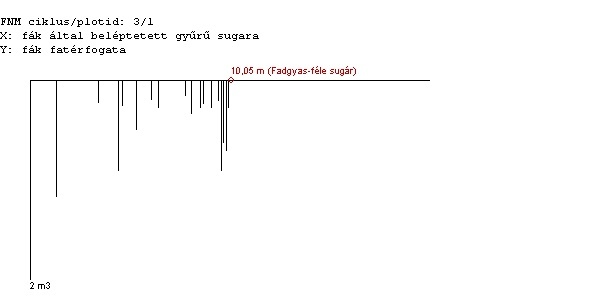
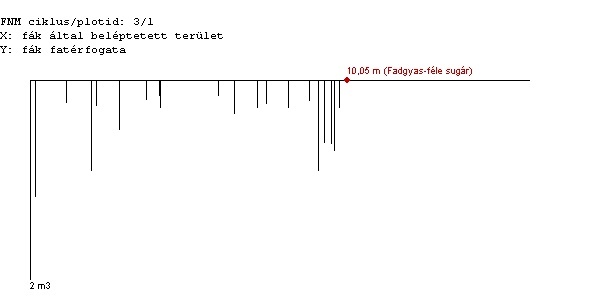
Az ábra tehát skálázható a fák középponttól mért távolságával is, ekkor kifelé haladva egyre sűrűbb vonalakat kapunk; és skálázható a belépő terület arányában is, ekkor a vonalak (a fák) nagyjából egyenletesen lépnek be.
Ezt megnéztem a gyakorlatban, írtam egy programot, ami lerajzolja így egy dimenzióban a mintaköröket, és pár százat átnéztem. A vonalkód-olvasó a SPAR-ban érezheti magát így.
(Az egyenletesség valószínűleg igazolható lenne az egyes fákhoz tartozó gyűrűk területének eloszlásainak vizsgálatával is.)
Példának csatoltam egy mintakör egy-egy ábráját. A függőleges tengelyen az adott fa fakészlete van, de ez most nem érdekes, csak a vonalak egymáshoz képest vett távolsága számít.