Mostan színes ábrákkal álmodok.
Időközben megtaláltam a cég archívumaiban annak az 1988-as kutatási jelentésnek a dokumentációját, aminek keretében Ifj. Gál János (jelenleg docens az Egyetemen) a régi nomogramokat legutoljára függvényesítette. Ezek szerint a régi nomogramok függvényesítésében 3 item alkotja a szerző munkásságát:
- TDK-dolgozat (1977): "Matematikai statisztikai módszer fatermési függvények paramétereinek meghatározására";
- diplomamunka (1980): "Fatermési függvények alkalmazása az üzemtervek számítógépes adatfeldolgozásában";
- kutatási jelentés (1988): "Fatermési függvények bevezetése az üzemtervek számítógépes adatfeldolgozásába".
A TDK-t nem láttam, de a kutatási jelentésben a diplomamunkához nagyon hasonló függvényalakkal dolgozik (Bachmann), az a különbség, hogy az utóbbiban harmadfokú tagok is vannak, illetve a fatermési osztály jellemzésére egy sima rang helyett (= az fto száma) egy valódi metrikus és folytonos változót használt: a siteindexet (SI, megegyezés szerinti korban elért állomány-átlagmagasság). A harmadfokú tagok érzékenyebbé tették a regressziót, ez az előnye, de egyben hátránya, mert egy kicsit hisztisebbé is (hajlamosabbak instabilitásra, főleg az értelmezési tartomány szélein fodrosodik). (Johann Cruyff, a kiváló holland labdarúgó egyik aranyköpése volt, hogy "minden előnynek megvan a maga hátránya". Bingó.) A siteindexre való átállás igen jó ötlet volt, sok szempontból.
Az a feltételezésem, hogy ebből a három munkából, már csak a tapasztalatok kumulációja miatt is, a harmadik a legjobb megközelítés, és a továbbiakban ezzel foglalkoztam.
A jelenleg a Szolgálatnál alkalmazott fatermési modellre az egyszerűség kedvéért gyakran hivatkozok úgy, hogy "a szalagmátix". Pontosabban a szalagmátrix volt az anyukája, mert szerintem már nem 100%-ig felel meg az informatikai feldolgozás hajnalán, kb. a '70-es években használt adatszerkezetnek, sőt. A jelenleg használt fatermési táblák gyanúm szerint torzítottak, mindenféle praktikus okokból bele-belenyúltak a fatermési táblákba, és már kibogozhatatlan, hogy miért, mit akartak ezekkel a módosításokkal. A rendszernek mindenesetre nem tett jót, az ilyen megoldások általában kezelik a megcélzott problémát, viszont okoznak három másikat.
Munkatársaimmal rögzítettük a Gál-féle függvényesített fatermési táblák 1988-as verziójának paraméterlistáját, hárman, függetlenül, összevetettük és egy elég megbízható paramétertáblát kaptunk. Aztán lekódoltam az egész rendszert, megírtam minden szükséges függvényt az alkalmazásához, úgyhogy már keresztbe-kasba mindent tudok számolni: magasság, ftk, SI bemenő paraméterekkel bármilyen változót; illetve magasságot adott korban és ftk-nál. Eleinte a SI-ftk egyenlet megoldására brute force numerikus közelítéseket használtam, ami tűrhető volt, de döcögős; és a dolgokat az tette kényelmessé igazán, amikor leprogramoztam a harmadfokú egyenlet valós gyökeit megadó Cardano-képletet, azóta fut minden, mint az olajozott istennyila. (A Cardano-képletet a 16-ik században fejlesztették itáliai kereskedők és számolóművészek, grat.)
(Ennek pl. olyan következménye is van, hogy a Veperdi mester által bemutatott, és az elmondása szerint az ERTI-ben a fatermési táblák vezérgörbéihez kvázi szabványként használt hasonló alakú, de ötödfokú egyenleteket csak numerikusan lehetne használni.)
Ifj. Gál a kutatási jelentés 15-ik oldalán táblánként megadja a SI alkalmazhatósági szélső értékeit, melyeken kívül a függvényeket nem szabad engedni. A függvényeket minden alkalmazásban meg kell védeni a hülye paraméterektől. De nincs a dolgozatban információ arról, hogy mi alapján határozták meg ezeket a határokat.
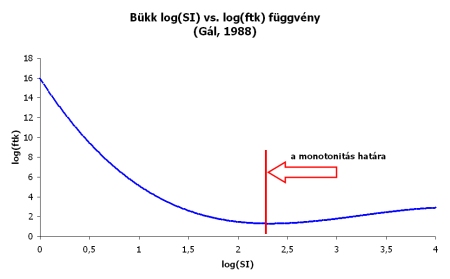
Saját felfedezésem, hogy az ftk-SI átalakító harmadfokú egyenlet miatt a SI-nek minden táblára létezik egy elméleti határa is. Az átalakító egyenletből az alkalmazástól függően mindkét mennyiséget ki kell tudni fejezni, tehát oda-vissza meg kell tudni oldani, s e szerint az SI-ftk harmadfokú egyenletnek az értelmezési tartományon monotonnak is kell lennie, azaz egy darab SI-értékhez egy darab ftk-értéknek kell tartoznia és viszont. Ez a korlát bizonyos táblák és a hozzájuk rendelt paramétersorok esetében elég szűk, több tábla esetében szűkebb, mint a kutatási jelentés 15-ik oldalán megadott határok, továbbá szűkebb, mint az eredeti nomogramokon használt ftk-határok (pl. bükk, nyír, feketefenyő). Az SI elméleti határait később úgy lőttem be, hogy vettem egy olyan pontot az értelmezési tartományon, ami minden táblánál értelmes volt (SI = 20m), és attól jobbra-balra megkerestem a függvény szélsőértékeit.
A következő lépés a függvények jóságának ellenőrzése volt - ezt a laikus, vizuális típusú testvérekre is való tekintettel úgy tűnt a legegyszerűbbnek megoldani, ha megrajzoljuk velük a nomogramokat. Ehhez tájékozni (mérethelyesre hozni) kellett az eredeti beszkennelt nomogram-nyomtatványokat, és az adott, negyedenként 87×130 mm-es keretbe belerajzolni a nívóvonalakat.
Vörös tölgy nomogram, ftk = 6-20 m3/ha/év és kor = 10-120 év tartományon. Ezek pontok, amiket látunk, de az öreg ArcView, ami kéznél volt az ábrázoláshoz, isten kegyelméből ilyen dollárjelekkel jelöli a pont-geometriákat. Rendes CAD-del ezek összeköthetőek rendes vonalakká. És még így is milyen szép a görbesereg. Akár ki is lehetne adni őket. Pl. a VT-nek egészen esztétikus, moarésodó és bugyborékoló vonalai vannak. A megfésült sündisznók esete. A szem más mintát lát a pontokban, mint az eredeti vonalak.
